Škola letecké meteorologie, 12. díl - Hustota vzduchu

Hmotné prostředí, to je to, co pro létání letadly potřebujeme. Ve vakuu nám aparát nepoletí.

Navíc je potřebné, aby se letadlo (ať už aerostat nebo aerodyn) vyskytovalo v prostředí tekutém, ideálně v plynu. Ne že by se vztlaková síla nedokázala vytvořit i ve vodě nebo ve rtuti, ale přece jen vzduch či jiný plyn s patřičnou hustotou je pro letadlo tak akorát.

Hustota prostředí je tedy vyjádřením množství hmoty v určitém objemu. Čím je vyšší hustota, tím více hmotných částic je v jednotkovém objemu. U aerodynamického letadla to znamená, že při určité rychlosti pohybu se přes nosné plochy převalí jisté množství, tj. jistá hmota vzduchu. Na rychlosti proudění potom závisí tvorba vztlaku, což je pilotům dobře známo. Máme-li stejnou rychlost, ale nižší hustotu, pak je generován nižší vztlak. S rostoucí výškou až na výjimky hustota vzduchu ubývá a s tím ubývá i vztlaková síla. Letadlo ve větší výšce musí proto letět rychleji, aby úbytek hustoty prostředí kompenzovalo. Tak může dostoupat až do takové hladiny, kde je hustota taková, že letadlo dosáhne maximální možné rychlosti letu a další stoupání už kvůli chybějícímu vztlaku není možné. Letadlo se ocitne na hranici dostupu. Dostup můžeme snadno spočítat z rovnice vztlaku, známé maximální rychlosti a hmotnosti letadla.

Nejprve se lehce seznámíme s několika procesy v plynech, kde hustota hraje určitou roli. Jedním je izobarický děj. Výraz „izobarický“ znamená, že tlak plynu se během tohoto děje nemění, je konstantní. Vezmeme-li stavovou rovnici (hustota se rovná tlak dělený měrnou plynovou konstantou a teplotou) a definici hustoty (hustota se rovná hmotnost dělená objemem), pak z těchto dvou vztahů dovodíme velmi jednoduše, že tlak plynu se bude rovnat součinu hmotnosti, měrné plynové konstanty a teploty, dělený objemem. Mějme válec s pístem, uvnitř prostoru je vzduch. Když do válce dodáme teplo, plyn začne expandovat a tlačit na píst, který se tím ve válci posouvá a koná práci. Přesně tohle dělá spalovací motor nebo parní stroj. Tlak uvnitř válce zůstává stejný. Sestavíme rovnici, kdy na jedné straně bude počáteční a na druhé koncový stav za předpokladu neměnného tlaku, pak dostaneme, že poměr teploty a objemu je po celou dobu procesu konstantní. Když potom dodané teplo unikne stěnami válce pryč, objem vzduchu se smrští a píst se posouvá zase na opačnou stranu.

Druhým procesem, v meteorologii dost užitečným, je děj adiabatický. Toto slovo vyjadřuje podmínku, že zkoumaný objem vzduchu či jiného plynu si nevyměňuje tepelnou energii s okolím, což v předchozím izobarickém ději bylo jinak. Je to něco jako termoska. Teplo, kterým vzduchová částice disponuje, zůstává konstantní, bez ohledu na to, jak se v částici mění objem nebo tlak. Ve zmíněném válci tentokrát nepohybuje pístem rozpínající se vzduch uvnitř, ale vnější síla. Třeba my. Taky jste jako malé děti zkoumali takové ty umělohmotné injekční stříkačky, které se pracně sháněly, abyste mohli po sobě stříkat vodou v klukovských bitvách? Když ve stříkačce byl vzduch a ucpali jste otvor, pak tahali za píst, tlak uvnitř klesal a vcucával ucpávající palec trošku směrem dovnitř. Když jste píst pustili, vracel se zpátky k výchozí poloze. Vyrobili jste podtlak. Tak to bylo působení vnější síly a ovlivňování hustotních poměrů uvnitř stříkačky. 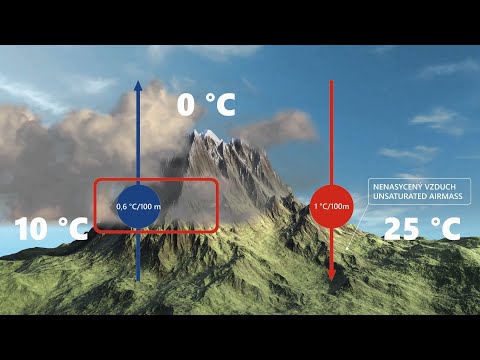Takhle nějak se chová i vzduchová částice, vystupující vertikálně atmosférou do výšky. Můžeme si ji představit jako vzduch uvnitř stříkačky, který se rozpíná, protože je okolním tlakem atmosféry postupně méně stlačován. Hustota uvnitř klesá, a kdybychom na proces aplikovali první větu termodynamickou, došli bychom k závěru, že klesá také tlak a teplota. Jestliže je ve vzduchu konstantní množství molekul vodní páry, dějou se tam zajímavé věci, které vedou až ke kondenzaci a vzniku oblačnosti.

Vlhkost ve vzduchu také ovlivňuje celkovou hustotu. Známe tři stavy vzduchu z hlediska obsahu vlhkosti. Suchý vzduch žádnou molekulu H2O neobsahuje, našli bychom v něm jen těch známých 78 % dusíku, 21 % kyslíku a jako šafránu helia, argonu, neonu a dalších vzácných plynů. Vlhký vzduch obsahuje jisté množství vodní páry, nikoli však maximální, které přísluší dané teplotě. A konečně vzduch nasycený, ve kterém je kapacita zcela naplněna a je zde maximální možné množství plynných molekul H2O. Při dalším nasycování by už docházelo ke kondenzaci a nadbytečné molekuly plynné H2O by se slučovaly do mikrometrických kapiček, tj. kapalné H2O. Vznikal by oblak, např. mlha. My v dnešním výkladu zůstaneme u vlhkého vzduchu. Protože Avogadrův zákon říká, že při dané teplotě a tlaku je v daném objemu vždy stejné množství molekul, které činí 6,022.1023, z čehož také plyne, že poměr hustot dvou plynů je roven poměru hmotností jejich molekul. Pokud do suchého vzduchu vpravíme molekuly H2O, pak je to výměnou za jiné molekuly dusíku nebo kyslíku. Molární hmotnost H2O je 18 gramů na jeden mol; molární hmotnost dusíku je 28 g/mol a kyslíku 32 g/mol. Vzdušná vlhkost tedy vede k nižší hustotě daného objemu a vlhký vzduch je proto lehčí, než vzduch suchý. Je to zdánlivý paradox, protože na první dojem by se zdálo, že když do vzduchu vpravíme vodu, bude těžší, resp. hustší. Nezaměňujme však jednotlivé molekuly vodní páry a kapalnou vodu.

Vertikální změna hustoty vzduchu v atmosféře je podobná změně tlaku. Klesá take logaritmicky, ale ne tak rychle, jako tlak. Příčinu naznačuje stavová rovnice. Hustota je přímo úměrná tlaku, ale nepřímo teplotě. S rostoucí výškou klesá tlak, ale i teplota (alespoň v troposféře). Tlak však klesá strměji, než teplota. Je však jeden speciální případ, kdy nastává inverze hustoty vzduchu — když teplota s výškou klesá strměji, než 3,4 °C/100 m, což je tzv. autokonvekční gradient. K takovému stavu dochází těsně u země v případě silně přehřátého podkladu. K tomu dochází u nás v horkém létě nad asfaltovými, betonovými a jinými plochami, které absorbují velké množství slunečního záření. Inverze hustoty je však jen v nepříliš silné vrstvě od země do výšky několika dm až m. I tak se může výjimečně stát, že letadlo, klesající na přistání, se při podrovnávání prosedne vlivem toho, že proklesalo do řidšího vzduchu na dráhou.

V Mezinárodní standardní atmosféře je ke každé výšce přiřazena hodnota teploty, tlaku a tím i hustoty. U hladiny moře je hustota 1,225 kg na metr krychlový a postupně s výškou ubývá. Kolem 10 km už je hustota vzduchu asi třetinová oproti úrovni moře a ve výškách 100 km se blíží nule. Čistě hypoteticky by ale nuly měla dosáhnout až kdesi v nekonečnu. Však i Mezinárodní kosmická stanice, kroužící kolem Země ve výšce 400 km nad úrovní moře, klade vzhledem ke své rychlosti asi 8 km/s jemný aerodynamický odpor, a v důsledku toho se nenápadně zbržďuje. Snížená rychlost potom vede k jejímu pozvolnému klesání do nižších výšek s rostoucí hustotou vzduchu, což by nakonec způsobilo shoření stanice ve výškách pod asi 120 km. Proto jednou za několik týdnů posádka stanice spustí raketové motory, aby stanici zvedli na vyšší orbitu.

V letectví je důležitým pojmem hustotní výška. To je výška, kterou bychom měli, kdyby nás obklopovala ISA, kdyby kolem nás nebyly aktuální poměry teploty a tlaku. To hraje důležitou roli např. při výpočtu délky rozjezdu letadla na dráze a strmosti jeho následného stoupání. Příkladem budiž letiště, které je v nadmořské výšce 500 m, tlak QNH je 980 hPa a teplota vzduchu na úrovni moře je 38 °C. Potom je ve výšce 500 m taková hustota, jaká by jinak za podmínek ISA byla ve výšce 1600 m. To je právě hustotní výška neboli density altitude. Kdyby byl vzduch až příliš řídký, mohlo by se stát, že by se letadlo rozjíždělo příliš dlouho, než by získalo potřebný vztlak. V extrému by nemusela ani stačit délka dráhy. To je známý problém vysoko položených letišť v tropických nebo subtropických oblastech, např. Mexico City. Dráhy musejí být dost dlouhé na to, aby letadla byla schopna bezpečně dosáhnout rychlosti vzletu vrotate. Krom toho je potřebné vypočítat rychlost v1, což je hraniční rychlost, ze které ještě lze rozjíždějící se letadlo zastavit do konce dráhy. Z vyšší rychlosti už by se to nestihlo a letadlo by při deceleraci vyjelo za dráhu. Při výpočtu v1 se musí zohlednit technické možnosti letadla, jako je účinnost brzd nebo reverzu motorů, hmotnost stroje, čelní složka větru a právě hustota vzduchu. Jsou známy případy z letiště LKPR, kdy v 80. letech 20. století byla dráha 25 (dnes 24) kratší než dnes, a v horkých letních dnech zde v odpoledních hodinách nebylo schopno odstartovat letadlo IL-62 společnosti Cubana kvůli vysoké teplotě vzduchu. Letadlo mělo velkou spotřebu paliva, bylo tudíž plně natankované na dlouhou cestu do Havany. Krom toho bylo plné cestujících s bagáží. Stávalo se, že odlet z Prahy byl zpožděn až do pozdních nočních hodin, kdy už bylo chladněji. Hustota vzduchu při teplotě 15 °C je o 7 % vyšší, než při 35 °C a se zohledněním parametrů akcelerace to může pro Iljušin znamenat několik stovek metrů delšího rozjezdu. Rozdíl hustot letního a zimního vzduchu, při teplotě 35 °C a -10 °C, je celých 17 %. To jistě bude znát každý pilot malého letadla na sportovním letišti, kdy při letním horku je o stejné procento méně účinná i vrtule a letadlo se vznese o poznání později, další roli hraje nižší účinnost pístového motoru.

RNDr. Petr Dvořák
Letecký meteorolog, lektor

www.jasno.cz